A Reinforcement Learning Approach to 5 in a Row
A Reinforcement Learning Approach to 5 in a Row
Technologies:
- Windows/Linux
- Python
- Keras
- C++
The task
5 in a row is a simple and popular board game played between two players where the objective is to chain exactly 5 of your pieces in a line to win. The game is typically played on a 15x15 board, though many play on a 19x19 board meant for playing Go instead.
Sample position that may arise in a game of 5 in a row. The piece with the red square was the last move to be made.
How can we make a computer play this game well?
The theory
You might have heard of Monte Carlo Tree Search (MCTS). It has one particular component - the random simulation used to approximate the value (i.e., the probability of winning) of a particular position. This has proven to work well with games like Go, with most to all of the state-of-the-art Go playing programs of the previous era using this approach.
However, this does not work well with games like Chess and 5 in a row, especially due to their extremely tactical nature - it isn’t abnormal to have positions where a completely winning position can become completely lost with just 1 move. This makes the random simulations often produce high-variance and inaccurate results, greatly hurting the playing strength of the program.
The solution is to replace the random simulations which return -1 for lost, +1 for won, and 0 for drawn with a neural network that returns some value between -1 and 1 approximating the winning chances of the position. This neural network is called the value net/network.
However, suppose you have 225 possible moves to play. You would need to evaluate all of them with the value network to figure out which move is best. So in addition to the value net, we use a policy net which returns the probabilities of a move to be played given an input position, assuming better moves have higher probability to be played. This neural network is called the policy net/network.
So to summarise:
| Neural network | Input | Output |
|---|---|---|
| Value net | Board position | Value from -1 to 1 representing expected outcome |
| Policy net | Board position | Probabilities of each move being played |
The question now turns to how we train those neural networks. The solution to this is run a handful of selfplay games where the AI plays against itself. To avoid a scenario where the pig blindly follows a carrot on a stick taped to its back (i.e., it becomes delusional because it is generating its own training data), select randomness is added to its selfplay games.
The training targets for the value net is the outcome of the game, and the training targets for the policy net is the number of playouts each move received during selfplay.
The plan
We first need to define the inputs to the neural network. Take the below position for example.
We use 3 key pieces of information:
- Where the black pieces are
- Where the white pieces are
- Whose turn it is to move
Each of these points gets represented as its own matrix ($6\times 6$ in this case).
Where the black pieces are:
\[P_B = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\]Where the white pieces are:
\[P_W = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\]Whose turn it is to move (white to move = all 0s, black to move = all 1s):
\[P_T = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\]These define our 3 input planes which are all $6\times 6$ matrices. By “stacking” them together, we get a single $3\times 6\times 6$ input tensor as the input to our neural network.
As side fact, you can visualise the inputs as the $6\times 6$ dimension being image width and height, and the 3 planes representing RGB. Whilst it may seem nonsensical to imagine representing a position in a 5 in a row game as an image, any human player will tell you that it’s all about the pattern recognition and intuition. In the same way, structuring the inputs like this preserves the spatial information about the game (where there could be connected pieces, etc.), which allows us to use image processing techniques such as convolutional neural networks which greatly improve playing strength.
There are many ways to define the neural network. The way described in the original paper uses a large convolutional stack where it then splits into two “heads” for the policy and value net outputs. I scale it down a lot to save resources. You can refer to this cheat sheet for a very nice visualisation on how a lot of this stuff works.
Now it’s time to define how the policy and value nets are going to be trained. After running the selfplay games, we have a collection of data points where we have a state $s$ (input tensor), the result $z$ (-1, 0, or 1), and search probabilities $\boldsymbol\pi$ as a normalised vector of the amount of visits each move got during selfplay. We can also get the neural network’s estimates of $z$ and $\boldsymbol\pi$ as $v$ and $\mathbf{p}$. The neural network update is to reduce the squared difference between $z$ and $v$, and the cross-entropy loss between $\boldsymbol\pi$ and $\mathbf{p}$.
\[\boldsymbol\pi = f_{policy}(s) \\ v = f_{value}(s)\] \[loss = (z - v)^2 - \boldsymbol\pi \cdot \log{\mathbf{p}}\]A L2 regularization term (typically 0.0001) is also applied to all the weights of the neural network. On top of that, we randomly flip/rotate positions in the training data to accelerate learning.
The implementation
Training was done on a preemptible virtual machine on Google Cloud Platform (GCP) which made it so that I didn’t have a whirring fan in my bedroom as I tried to sleep, on top of being cheap.
At first, we can see its training games are pretty random. (Click the left and right side of the board to replay the game.)
We can also see that it’s pretty clueless. The darker the blue circles are, the more consideration the AI is giving to the move.
You can see that its play is extremely short sighted - its top two moves are both easily refutable, it seems to consider many nonsensical moves, and does not consider what I believe to be a winning combination starting with the move outlined in green.
Later on in training, we can see it play some more ordinary looking games.
And in this position, it is able to spot a combination that wins the game.
You can see how it diverts nearly all of its time into thinking about moving to the winning move, despite the win being relatively distant.
In fact, we can revisit the previous position and ask the AI what it thinks now.
Indeed, it correctly finds the winning move.
More impressively, it is able to this almost instantly. In fact, here is the policy net’s output:
Without any calculation, the neural network by some magical “intuition” just knows where it should put its pieces.
Well now it’s time to have some fun right?
Let’s ask the policy what the best response to the typical first move is.
I personally like to move immediately diagonal for my first move because that’s what you do in tic-tac-toe but maybe I will need to change my ways now.
Maybe I should play some games against it. (I’m playing black in all the games).
Looks like I’m just too good.
Nevermind, though this is also a pretty fun game to play: You are versing me, white to play. Can you find the winning tactic in this position?
Hint: this is the policy net’s output:
And if we get it to search the position…
info nodes 50 value 0.287770 pv L10 L9 K10 K11 J10 M7 M6
info nodes 100 value 0.395997 pv L10 L9 K10 K11 J10 M7 M6 I4 I3
info nodes 150 value 0.437160 pv L10 L9 K10 K11 J10 M7 M6 I4 I3 M4
info nodes 200 value 0.494264 pv L10 L9 K10 K11 J10 M7 M6 I4 I3 M10
info nodes 700 value 0.677791 pv K10 K11 L10 L9 J10 M7 M6 I4 I3 M10
info nodes 750 value 0.648769 pv K10 K11 L10 L9 J10 M7 M6 I4 I3 M4 N3
info nodes 800 value 0.636061 pv K10 K11 L10 L9 J10 M7 M6 I4 I3 M4 N3 J5
info nodes 900 value 0.629300 pv K10 K11 L10 L9 J10 M7 M6 I4 I3 M4 N3 J5 K5
info nodes 1600 value 0.622272 pv L10 L9 K10 K11 J10 M7 M6 I4 I3 M4 N3 J5 K5
info nodes 1850 value 0.599837 pv L10 L9 K10 K11 J10 M7 M6 I4 I3 M4 N3 J5 K5 H3 G2
info nodes 5650 value 0.538424 pv L10 L9 K10 K11 J10 M7 M6 I4 I3 M4 N3 J5 K5 H3 G2 J4
info nodes 6400 value 0.526216 pv L10 L9 K10 K11 J10 M7 M6 I4 I3 J5 K5 H3 G2 M10 M11
info nodes 8000 value 0.634462 pv L10 L9 K10 K11 H10 I9 J10 I10 I11 M7 H12
info nodes 20000 value 0.903950 pv L10 L9 K10 K11 H10 I9 J10 I10 I11 M7 H12
bestmove L10
And actually, I think all of the circled moves win.
There might be more wins, though they probably take longer. After you play those moves in any order, and black tries to defend their immediate threats, the killshot is obvious even to the policy net, which reports that the circled move has a $96.7\%$ chance to be optimal.
The results
Training statistics
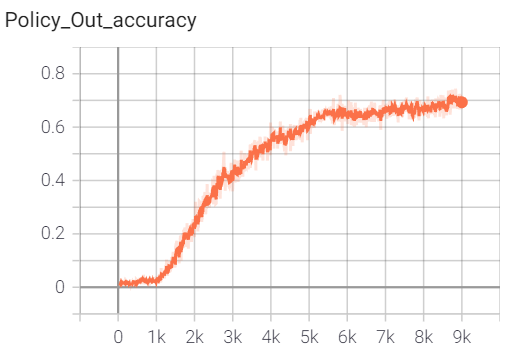
The policy net is able to predict the best move out of a sea of hundreds of moves with a 70% accuracy.
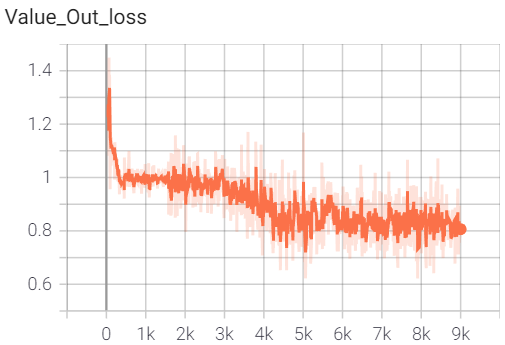
The value net provides a somewhat noisier estimate of the position’s expected outcome, but its evaluations are still critical for guiding search.
Household internal rankings
| Rank | Player |
|---|---|
| 1 | Me |
| 2 | AI |
| 3 | The little bastard |
| 4 | Mum |
| 5 | Granny |
| 6 | Dad |
Afterword
This isn’t my first rodeo into making computers teach themselves simple games - I’ve done it before with Connect-4 (don’t judge my code there - it’s very old) and Othello too. Likewise, I doubt it would be my last, as doing a project like this always teaches me plenty of stuff about machine learning, machine learning frameworks, and whatever language I’m using such as C++. In the future, I would like to open source this project, but not before I improve the quality of the code so that I’m happy with it.
Perhaps unsurprisingly, there’s plenty of projects like this one on the internet with some of them backed by large communities. My favourite are:
There’s also a nice read in KataGo’s docs where they describe how to train a single neural network to handle arbitrarily sized inputs (so it can play on both 15x15 and 19x19 boards), which I might try to do with this game one day.